기계 학습은 데이터의 특성에 따라 사용하는 모델이 달라진다.
그래서, 데이터의 특징을 살펴보고 여기에 적절한 모델을 선택하면 된다!
다양한 머신러닝 모델
1) 서포트 벡터 머신
2) 랜덤 포레스트(decesion tree를 우선으로)
3) 그레이디언트 부스팅
4) 에이다 부스트
등등이 있다.
오늘은 서포트 벡터 모델을 사용해보려한다!
1. 기본 개념 복습하기!
인공지능 - 규칙을 찾는 것
기계학습 - 학습을 하는 것
딥러닝(신경망) - 신경망 방식으로 학습을 하는 것
인공지능은 매우 큰 개념이고 그 안에 기계학습이 있고 그 안에 딥러닝이 있다고 이해하면 쉽다.
기계학습은 (1)회귀(선형, 비선형)과 (2)식별(2개,3개...n개)로 나눌 수 있다.
2. 학습 과정
머신러닝의 학습 과정은 아래의 4가지 단계를 거친다.
(1)데이터 수집 - (2)학습(방법 + 인자조절) - (3)평가 - (4)학습모델완성
중요한 것은 데이터에 적합한 모델을 선택하는 것이고, 그 후 인자를 적절하게 조절하는 것이다.
3. 파이썬에서 머신러닝을 실습할 때 필요한 모듈
그래프 분포 등을 표현하는 모듈 : seaborn
인공지능 관련 학습 모듈 : sklearn
다양한 표와 그래프 : pandas
파이썬에서 머신러닝을 실습할 때는 위의 모듈이 필요하며 미리 import를 해주어야 한다.
가장 중요한 sklearn의 경우 사이트에서 여러 예제들을 확인하며 연습해볼 수 있다.
scikit-learn모듈의 예제
scikit-learn.org/stable/auto_examples/index.html

4. 서포트 백터 머신(Support Vector Machine)
서포트 백터 머신은 예측 모델 중에 가장 강력한 모델이라고 할 수 있다.
scikit-learn 사이트에 가면 다양한 서포트 벡터 머신의 다양한 모습을 확인할 수 있다.

아래의 그림은 서포트 벡터 머신의 원리를 설명하는 그림인데
사실 잘 이해는 안간다.
어찌되었든 빨간 데이터와 파란 데이터 사이의 마진을 적절히 조절하며 적합한 모델을 만드는 것이라 이해하면 쉽다.
1) 가우시안 커널
2) 모든 차수의 모든 다항식 고려
3) 두 데이터 사이 거리를 구하기
두 데이터 사이 거리
Polynomial(nomogeneous)
Plynomial(inhomogeneous)
등등의 개념이 있는데....깊게 이해는 힘들기 때문에... 바로 활용으로 넘어가보자!

5. 서포트 백터 머신 사용 옵션
서포트 백터 머신을 사용할 때 고려해야할 다양한 옵션은 아래와 같다.
linear : 데이터를 구별할 때 리니어한다.
poly : 2차,3차식을 만들 수 있다.
Radical basis function : 가능한 구별할 수 있는 선을 다양하게 그려볼 수 있다.
실제로 서포트 백터 머신을 사용해보자!
먼저 x데이터와 y데이터를 만들어야한다.
x값은 랜덤으로 0부터 1사이의 소수 100개이다.
그 값에 10을 곱하고 5를 빼준다.
y값은 삼각함수의 sin값으로 x값들의 모든 sin값들을 구한다. 값은 -1에서 1사이의 값을 갖는다.
그 값에 랜덤 숫자를 더해준다.
import matplotlib.pyplot as lot
import numpy as np
import math
x = np.random.rand(100,1)
x = x * 10-5
print(x)
y = np.array([math.sin(i) for i in x])
print(y)
#평균 0 표준편차 1인 가우시안 정규 분포
y = y + np.random.randn(100)
print(y)
6. LinearRegression으로 x와 y 관계 예측
LinearRegression으로 그려보아도
결정계수가 크지 않은 것을 볼 수 있다.
결정계수가 0.002로 거의 규칙성을 찾기가 힘들다.
import matplotlib.pyplot as lot
import numpy as np
import math
x = np.random.rand(100,1)
x = x * 10-5
y = np.array([math.sin(i) for i in x])
#평균 0 표준편차 1인 가우시안 정규 분포
y = y + np.random.randn(100)
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x, y)
print('기울기 a :', model.coef_)
print('y절편 b: ', model.intercept_)
relation_square = model.score(x, y)
print('결정계수 r : ', relation_square)

7. sklearn.svm 으로 x와 y 관계 예측
반면에 서포트 백터 머신을 쓰면
결정계수 r이 0.34로 LinearRegression보다 훨씬 결정계수가 높다.
서포트 백터 머신은 from sklearn.svm import SVR
이렇게 사용하면 된다.
LinearRegression처럼
1) 모델을 만들고
2) 피팅하고
3) 결정계수를 구한다.
그 다음 y_p라는 예측 모델을 만든다.
+로 나타난 것은 원래 데이터이고 o로 나타난 것은 예측 데이터의 모습이다.
o를 보면 sin함수의 모습을 띄고 있다.
import matplotlib.pyplot as plot
import numpy as np
import math
x = np.random.rand(100,1)
x = x * 10-5
y = np.array([math.sin(i) for i in x])
#평균 0 표준편차 1인 가우시안 정규 분포
y = y + np.random.randn(100)
#서포트 백터 머신 모듈 가져오기
from sklearn.svm import SVR
model = SVR()
model.fit(x,y)
relation_square = model.score(x, y)
print('결정계수 R :', relation_square)
y_p = model.predict(x)
plot.scatter(x, y, marker = '+')
plot.scatter(x, y_p, marker = 'o')
plot.show()
8. 반복문으로 linear, rbf, poly옵션 각각 돌려보기
이번에는 반복문으로 linear, rbf, poly 옵션을 각각 알아보자!
SVR에 kernel 로 옵션을 설정할 수 있다. 옵션이 바뀜에 따라 결정계수는 어떻게 나올까?
linear일때와 poly일때보다 확실히 rbf옵션일 때 결정계수가 높았다.
rbf는 0.401로 나왔고
랜덤 값들로 알아보는 것이기 때문에 수행할 때마다 결정계수는 다르게 나온다.
import matplotlib.pyplot as plot
import numpy as np
import math
x = np.random.rand(100,1)
x = x * 10-5
y = np.array([math.sin(i) for i in x])
#평균 0 표준편차 1인 가우시안 정규 분포
y = y + np.random.randn(100)
from sklearn.svm import SVR
for i in ('linear', 'rbf', 'poly'):
model = SVR(kernel = i)
model.fit(x, y)
relation_square = model.score(x, y)
print('결정계수 R : ', relation_square)
y_p = model.predict(x)
plot.scatter(x, y, marker = '+')
plot.scatter(x, y_p, marker = 'o')
plot.show()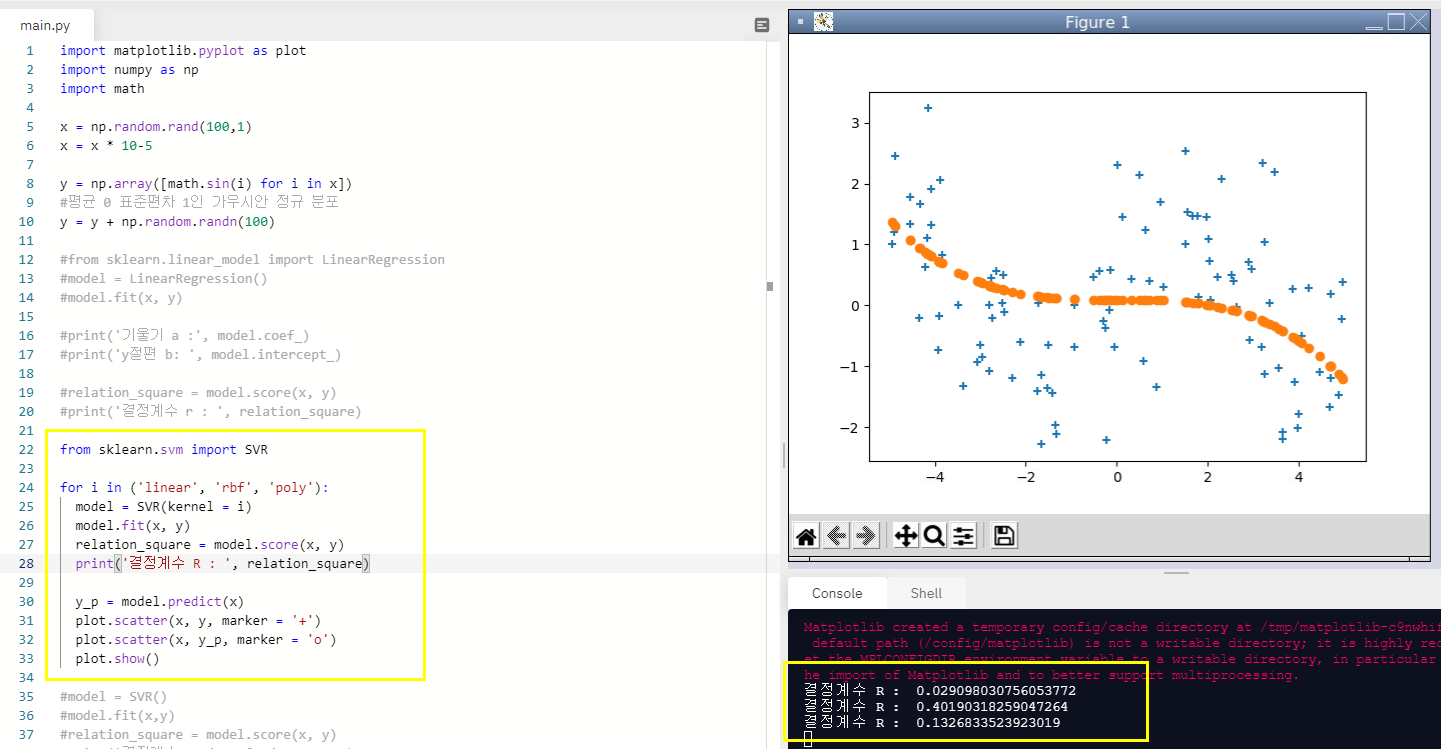



SVR은 앙상블 모델 중 가장 강력한 모델인 듯 하며 특히 rbf 옵션을 사용할 때가 결정계수가 가장 높다!
'프로그래밍 > 머신러닝' 카테고리의 다른 글
| 랜덤 포레스트(RandomForestRegressor)_파이썬으로 머신러닝 배우기 (2) | 2021.04.26 |
|---|---|
| 서포트 백터 머신(model = SVR(kernel = 'rbf', C=1000, gamma = 1000)_파이썬으로 머신러닝 배우기 (0) | 2021.04.23 |
| 집값과 경기종합지수의 상관관계_파이썬으로 머신러닝 배우기 (0) | 2021.04.19 |
| 삼성전자, 현대자동차, LG화학 주가와 KOSPI 주가의 상관 관계 분석_파이썬으로 머신러닝 배우기 (0) | 2021.04.16 |
| 다중 선형 회귀_파이썬으로 머신러닝 배우기 (0) | 2021.04.14 |



