이번글에서는 SVR의 kernel 'rbf'의
c옵션과 gamma옵션에 대해 알아보자!
C와 gamma값이 바뀔 때 결정계수가 다르게 나오는데 어떻게 바꾸어야 결정계수가 크게 나오는지 실험해보려한다!
1. C와 gamma는 무엇일까?
c 는 제약 조건이며
0.1 : 매우 제약조건이 큰 경우
100 : 제약조건이 작은 경우
로 이해하면 된다.
gamma는
가우시안 커널의 반경을 크게 또는 작게할 것인지를 의미한다.
사실...c와 gamma가 정확히 무엇인지는 잘 모르겠다.
2. 실전 c와 gamma 조정!!
C값이 0.1일 때 gamma값을 0.1, 1, 10, 100, 1000으로 바꾸어가며 결정계수를 확인해보고
그리고 C값이 1일 때 gamma값을 바꾸어가며 결정계수를 확인해보자.
이런식으로 C값이 0.1~ 1000으로 바뀔때마다 gamma값이 바뀌는 경우(즉, 25개의 경우)를 반복문을 통해 확인해본 뒤
어떤 경우가 결정계수가 가장 큰지 알아보자.
import matplotlib.pyplot as plot
import numpy as np
import math
x = np.random.rand(100,1)
x = x * 10-5
y = np.array([math.sin(i) for i in x])
y = y + np.random.randn(100)
from sklearn.svm import SVR
for i in (0.1, 1, 10, 100, 1000):
for j in (0.1, 1, 10, 100, 1000):
model = SVR(kernel = 'rbf', C=i, gamma = j)
model.fit(x, y)
relation_square = model.score(x, y)
print('결정계수 R : ', relation_square)
y_p = model.predict(x)
plot.scatter(x, y, marker = '+')
plot.scatter(x, y_p, marker = 'o')
plot.show()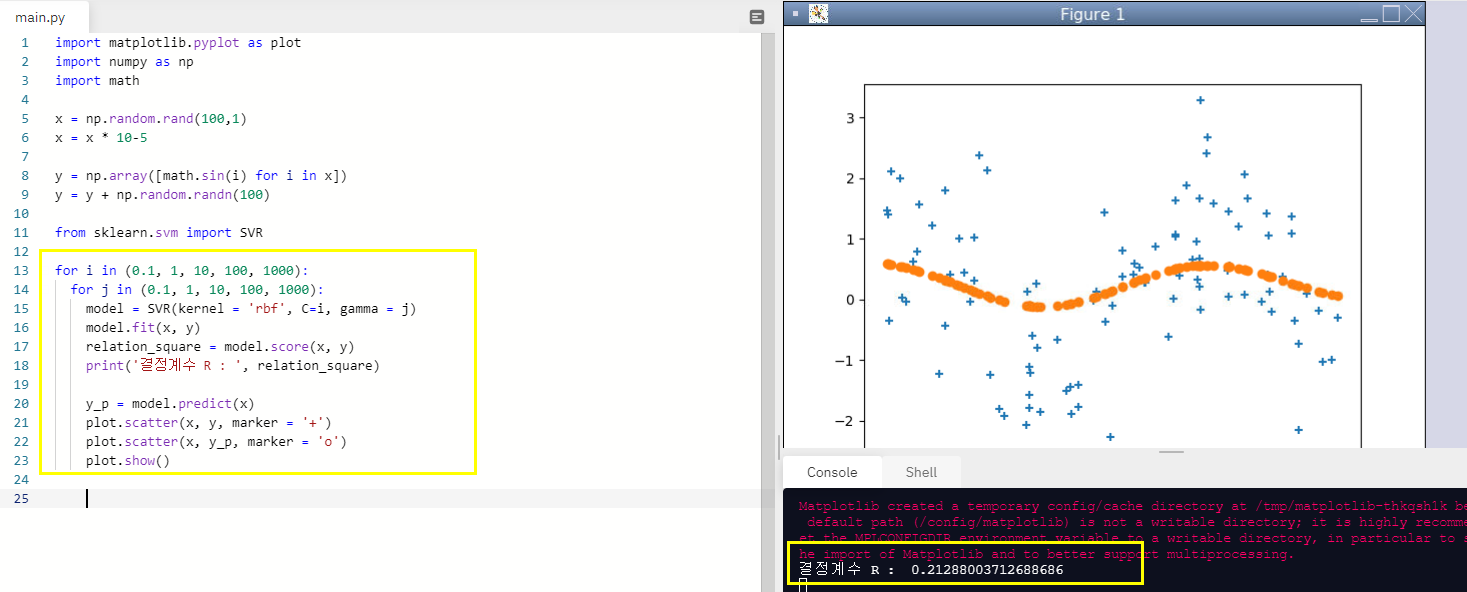
c와 gamma의 값이 각각 1000일때 결정계수는 0.920까지 올라간 것을 볼 수 있다!
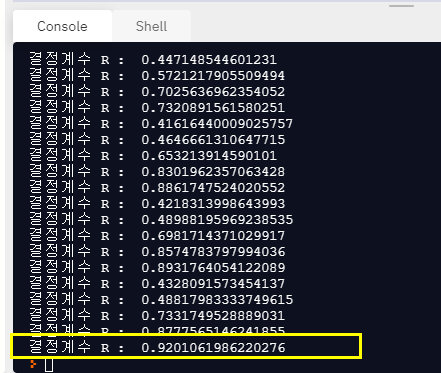
3. 수학 점수로 총점 예측하기
이번에는 수학 점수로 총점을 예측해보자!
x는 수학 점수
y는 총점으로 놓고 예측 모델을 만든다!
import matplotlib.pyplot as plot
import numpy as np
import math
import pandas as pd
import openpyxl
plot.rcParams["font.family"] = 'Malgun gothic'
data = pd.read_excel("student.xlsx", header=0)
newData = data[['kor', 'eng', 'math', 'social', 'science', 'total']]
#속성(변수) 선택
x = newData[['math']]
y = newData[['total']]
from sklearn.svm import SVR
import seaborn as sns
for i in (0.1, 1, 10, 100, 1000):
for j in (0.1, 1, 10, 100, 1000):
model = SVR(kernel = 'rbf', C=i, gamma = j)
model.fit(x, y)
relation_square = model.score(x, y)
print('결정계수 R : ', relation_square)
y_p = model.predict(x)
ax1 = sns.distplot(y, hist = False, label = 'y실제')
ax2 = sns.distplot(y_p, hist = False, label = 'y예측')
plot.show()
plot.close()

4. 국, 수, 사, 영어 점수로 총점 예측하기
import matplotlib.pyplot as plot
import numpy as np
import math
import pandas as pd
import openpyxl
plot.rcParams["font.family"] = 'Malgun gothic'
data = pd.read_excel("student.xlsx", header=0)
newData = data[['kor', 'eng', 'math', 'social', 'science', 'total']]
#속성(변수) 선택
x = newData[['kor', 'eng', 'math', 'social']]
y = newData[['total']]
from sklearn.svm import SVR
import seaborn as sns
for i in (0.1, 1, 10, 100, 1000):
for j in (0.1, 1, 10, 100, 1000):
model = SVR(kernel = 'rbf', C=i, gamma = j)
model.fit(x, y)
relation_square = model.score(x, y)
print('결정계수 R : ', relation_square)
y_p = model.predict(x)
ax1 = sns.distplot(y, hist = False, label = 'y실제')
ax2 = sns.distplot(y_p, hist = False, label = 'y예측')
plot.show()
plot.close()
SVR 진짜 대박이다. 결정계수가 0.999996이 나왔다.
어마어마한 예측률을 보인다.

SVR은 매우 강력한 예측 모델이며 그 중에서도 rbf는 결정계수가 매우 높은 것을 볼 수 있다!
'프로그래밍 > 머신러닝' 카테고리의 다른 글
| 그레이디언트 부스팅(GradientBoostingRegressor)_파이썬으로 머신러닝 배우기 (0) | 2021.04.26 |
|---|---|
| 랜덤 포레스트(RandomForestRegressor)_파이썬으로 머신러닝 배우기 (2) | 2021.04.26 |
| 서포트 백터 머신(from sklearn.svm import SVR)_파이썬으로 머신러닝 배우기 (1) | 2021.04.21 |
| 집값과 경기종합지수의 상관관계_파이썬으로 머신러닝 배우기 (0) | 2021.04.19 |
| 삼성전자, 현대자동차, LG화학 주가와 KOSPI 주가의 상관 관계 분석_파이썬으로 머신러닝 배우기 (0) | 2021.04.16 |



